Computer Vision
13.7. Depth

Depth is a critical part of computer vision, which gives the computer information about the distance of objects to the camera. Depth is used in applications like video games, such as Microsoft's Kinect, and aerial surveys. Another significant application is self-driving cars, which need to know how far away the vehicle ahead of it is to avoid collisions. One way of obtaining depth information is through stereo vision, which uses two cameras, usually side by side. Both cameras take a picture of the same scene. Objects that appear in both images will be at different positions, where the disparity is the difference between the positions. Objects close to the cameras will have a larger horizontal disparity in the images, whereas faraway objects will have a smaller disparity. Humans and many other animals also use this technique to obtain depth information. Each eye sees a slightly different image which the brain uses to tell whether an object is close or far away.

One possible method of programmatically obtaining the distance to an object from stereo images is detailed below. Other methods may provide better or worse results, but the following one is (relatively) simple. For those looking to learn more, the full paper this was inspired by can be found here. This section only considers the situation where the object is horizontally between the two camera positions.

An aspect of the camera we need to know is its angle of view. This value is the horizontal angle that the camera can see. If you cannot find the technical specifications of your camera, there is an easy way to obtain this. Prop a ruler up horizontally. Then, take a picture of the ruler, aligning the start of the ruler with the left edge of the photo. Ensure that ruler fills the entire photo (the right end is not visible). Also, measure the distance between the camera and the ruler (e.g. by using another ruler). An example picture is shown below.

As seen in the diagram above, finding the angle of view becomes a simple trigonometry problem. We derive the following equation for calculating the half angle of view.

$$\theta = \tan^{-1}\frac{r}{2d}$$

$r$ is the length of the ruler visible in the picture. $d$ is the distance from the camera to the ruler. Doubling the half angle of view gives us the full angle of view, $\theta_0$. When using the camera for the next part, you should use the same camera settings (e.g. zoom level) to ensure the angle of view does not change. Below is a calculator to calculate the angle of view.

Typically, a stereo vision system would use two identical cameras, but you can simulate this with one camera by taking two photos of a still object. Take two stereo pictures of an object where it is between the two camera positions. Use the same camera to take both images. The diagram below shows the setup. For both pictures, the camera should be pointing in the same direction such that the axes of view are parallel (or as close as you can get). A possible way of ensuring they are as parallel as possible is to align the camera with a straight line on the floor. Note down the distance between the camera positions and the actual distance to the object with rulers or measuring tape.

$\theta_0$ is the camera angle of view, which is the same for both cameras as you used the same camera for both pictures. $B_1$ and $B_2$ are the distances between the centre of the object and the left and right camera, respectively. Their sum is $B$, the distance between the cameras. $\theta_1$ and $\theta_2$ are the angles between the camera's axis of view and the line going from the camera to the object. Finally, $D$ is the distance to the object.

Derivation of the formula

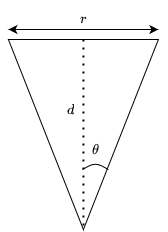
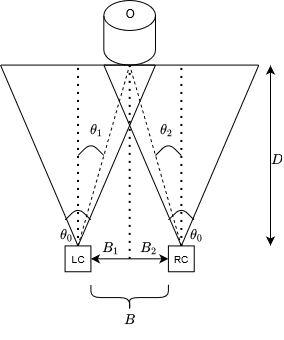
The left camera, LC, the right camera, RC, and the object, O, form a triangle. This triangle is comprised of two right-angle triangles as shown below.

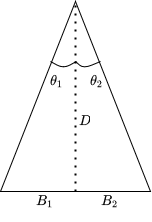
From basic trigonometry, it is known that $θ_1$ and $θ_2$ are the same as those in Figure 1. Using trigonometry, the following can be derived:

$$B_1 = D tan \theta_1\\ B_2 = D tan \theta_2$$

Therefore:

$$B = D tan \theta_1 + D tan \theta_2\\ B = D(tan \theta_1 + tan \theta_2)$$ $$D = \frac{B}{tan \theta_1 + tan \theta_2} \tag{1}$$

The following diagram shows the two camera views taken out from the first diagram for clarity. Think of each image as a grid, where the origin is the centre of the image.

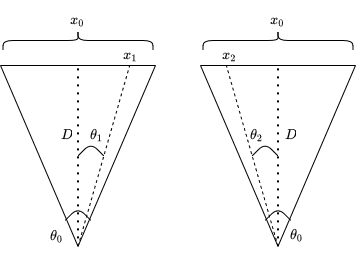
$x_0$ is the width of the image in pixels. The terms $x_1$ and $x_2$ are the x-coordinates of the object in the left and right images, respectively. As an example, consider the left view. There are two right-angle triangles, both of which share the side $D$. The smaller triangle has a top that goes up to the $x1$ point. $x1$ is also the top's length, as it is the x-coordinate where the centre is the origin. The larger triangle has a top that goes up to the end of the image. Using the smaller triangles in both views, we know the following using some basic trigonometry.

$$D = \frac{x_1}{tan\theta_1}\\ \tag{2}$$ $$D = \frac{-x_2}{tan\theta_2} \tag{3}$$

We negate $x_2$ as widths should be positive. Now consider the larger triangles. As they go up to the end of the image, the width of their tops are half of the image width, $x_0$. More trigonometry ensues.

$$D = \frac{\frac{x_0}{2}}{tan\frac{\theta_0}{2}} \tag{4}$$

Equating equations (2) and (4), we get:

$$\frac{x_1}{tan\theta_1} = \frac{\frac{x_0}{2}}{tan\frac{\theta_0}{2}}\\ tan\theta_1 = x_1 \div \frac{\frac{x_0}{2}}{tan\frac{\theta_0}{2}}$$ $$tan\theta_1 = \frac{2 x_1 tan \frac{\theta_0}{2}}{x_0} \tag{5}$$

Similarly, equating equations (3) and (4), we get:

$$\frac{-x_2}{tan\theta_2} = \frac{\frac{x_0}{2}}{tan\frac{\theta_0}{2}}\\ tan\theta_2 = -x_2 \div \frac{\frac{x_0}{2}}{tan\frac{\theta_0}{2}}$$ $$tan\theta_2 = \frac{-2 x_2 tan \frac{\theta_0}{2}}{x_0} \tag{6}$$

We're nearly there! Adding equations (5) and (6) gives:

$$tan\theta_1 + tan\theta_2 = \frac{2 x_1 tan \frac{\theta_0}{2}}{x_0} + \frac{-2 x_2 tan \frac{\theta_0}{2}}{x_0}$$ $$tan\theta_1 + tan\theta_2 = \frac{2 tan \frac{\theta_0}{2} (x_1 - x_2)}{x_0} \tag{7}$$

Substituting (7) back into (1) gives us our final equation.

$$D = \frac{B x_0}{2 tan \frac{\theta_0}{2} (x_1 - x_2)}$$

$(x_1 - x_2)$ is the disparity of the objects in the pictures. However, the disparity will be the same no matter what we choose as the origin of the coordinate system. Therefore, we can treat $x_1$ as the x-coordinates of the object from the left of the left image. Similarly, $x_2$ is the x-coordinates of the object from the left of the right image. To summarise, we can determine the distance to an object using only the following:

• The distance between the cameras, $B$.
• The width of the images in pixels, $x_0$.
• The angle of view, $\theta_0$.
• The x-coordinates of the object in the images, $x_1$ and $x_2$.

The following interactive shows the equation in action.

Distance from stereo images