Working with big numbers
Teacher Note
The following section relies on students using the built-in interactive to experiment with the calculations on the huge numbers that come up with the intractable problems.
This may be best run as a class activity where students are guided through calculating the stupendously big numbers that come up, and they should be encouraged to appreciate how impractical the amount of time taken by a program would be. For example, a program that takes a million years to find a solution won't be of any interest to the person who started it running, and even if a computer turned up that is 1000 times as fast, it would still take 1000 years to complete.
Some of the times that turn up below are so long that they are beyond our ability to imagine, and are best illustrated by seeing how futile the times are even with 1000, a million or even a billion times the computing power.
An earlier version of this chapter provided the following spreadsheet for doing these calculations; we've retained the link here for the meantime, but the new online interactive can cope a lot better with the large numbers in the calculations.
If you are interested, you can download the spreadsheet here to do the calculations:
There's a very simple rule that computer scientists use to decide if an algorithm is tractable or not, based on the complexity (estimated number of steps) of the algorithm.
Essentially, if the algorithm takes an exponential amount of time or worse for an input of size , it is labelled as intractable.
This simple rule is a bit crude, but it's widely used and provides useful guidance.
Note that a factorial amount of time, , is intractable because it's bigger than an exponential function.
To see what this means, let's consider how long various algorithms might take to run.
The following interactive will do the calculations for you to estimate how long an algorithm might take to run.
You can choose if the running time is exponential (that is, , which is the time required for the Towers of Hanoi problem with disks), or factorial (that is, , which is the time required for checking all possible routes a travelling salesperson would make to visit places other than the starting point).
You can use the interactive below to calculate the time.
For example, try choosing the factorial time for the TSP, and put in 20 for the value of (i.e. this is to check all possible travelling salesperson visits to 20 places).
Press the return or tab key to update the calculation.
The calculator will show a large number of seconds that the program will take to run; you can change the units to years to see how long this would be.
Solution
Teacher Note
With the initial settings in the interactive, the TSP for 20 places will take 2,432,902,008,176,640,000.00 seconds, which is 773,056,638.51 centuries (note that the calculator needs to be set to n! to apply to the TSP).
By the way, we're giving very precise numbers here just so that you know you have the right calculations in place; in practice the estimate is very crude, and rather than 773,056,638.51 centuries, it's just as accurate to say "about 770 million centuries", or even just "hundreds of millions of centuries".
It may be more meaningful to students it this is converted to some geological time frame.
So far the calculation assumes that the computer would only do 1 operation per second; try changing to a million (1,000,000) operations per second, which is more realistic, and see how long that would take.
Solution
Teacher Note
When the computer is a million times faster, the time for TSP on 20 places reduces from 773,056,638.51 centuries to 773.06 centuries.
It's still completely impractical!
Another way to solve problems faster is to have multiple processors work on different solutions at the same time.
If you were to buy 1,000 processors (e.g. 1,000 computers, or 250 4-core computers) and have each one test out different routes, then the solution could be found 1,000 times faster.
Try changing the number of processors to 1,000 and see how long that would take (you may need to change the units back).
Is it seconds? Hours? Days?
Solution
Teacher Note
1,000 processors reduces the running time to 77.31 years.
That's still too much computing power to be practical, but it's starting to get into the region where it's not completely impossible.
The interactive above estimates the amount of time taken for various algorithms to run given values to be processed.
Let's assume that we have a very fast computer, faster than any that exist.
Try putting in the assumption that the computer can do a million million (1,000,000,000,000) steps per second.
Is a solution achievable?
But what if you add just two more locations to the problem (i.e. =22 instead of =20)?
Solution
Teacher Note
This incredibly high speed would reduce the time to 40.55 seconds.
However, increasing the problem to just 22 cities blows it out again to 13.01 days.
The main point is that even if you get a massively fast bank of computers that can solve a particular problem, just adding a few items to the problem will put it out of reach again.
Now, consider an algorithm that has a complexity of (there are lots that take roughly this number of steps, including selection sort which was mentioned earlier).
Type in a value of 1,000,000 for to see how long it might take to sort a million items on a single processor (keep the number of steps per second at 1,000,000,000,000, but set the number of processors to just 1) – it should show that it will only take about 1 second on our hypothetical very fast machine.
Now put in 10 million for – although it's sorting a list 10 times as big, it takes more than 10 times as long, and will now take a matter of minutes rather than seconds.
At what value of does the amount of time become out of the question – that is, how large would the problem need to be for it to take years to finish?
Is anyone ever likely to be sorting this many values – for example, what if for some reason you were sorting the name of every person in the world, or every base in the human genome?
Solution
Teacher Note
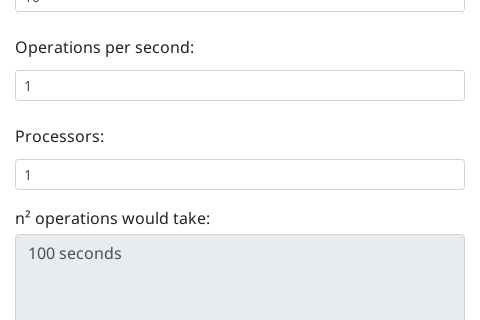
The algorithm with 10 million items takes 100 seconds above (each time n is multiplied by 10, it will take 100 times as long).
When n is a thousand million, it takes nearly 12 days, at which point you might consider it to be out of the question.
At n=10,000,000,000 it takes about 3.18 years, which is likely to be longer than a computer could run for continuously.
But that's a pretty big number of items to process – for example, it's big enough to cope with the population of the whole world.
And there's room for improvement by using a reasonable number of multiple processors.
What about an algorithm with complexity of ?
What's the largest size input that it can process in a reasonable amount of time?
Solution
Teacher Note
The algorithm can process 1,000,000 items in 11.57 days.
A million is nothing near the population of the world, or even a lot of countries, but a lot of real life problems are smaller than that.
Now try the same when the number of steps is , but start with a value of 10 for , then try 30, 40 , 50 and so on.
You'll probably find that for an input of about 70 items it will take an unreasonable amount of time.
Is it much worse for 80 items?
Solution
Teacher Note
The algorithm is in a completely different league to the previous ones.
10 items take a fraction of a second (1.02 nanoseconds to be precise), and 60 items take 13.34 days, but just 70 items blows out to 37.51 years, and 80 items takes 384 centuries.
Small increases in the number of items (eg. cities for the TSP to visit) result in HUGE increases in the time taken to evaluate them all.
Now try increasing the number of operations per second to 10 times as many.
Does this help to solve bigger problems?
Solution
Teacher Note
10 times faster reduces 384 centuries to 38.4 centuries - much faster, but it is still an impossibly large amount of time.
The lesson is that the algorithm will be so slow that even massive improvements in hardware won't have a useful impact.
By trying out these figures you will likely have encountered the barrier between "tractable" and "intractable" problems.
Algorithms that take , or even time to solve a problem (such as sorting a list) aren't amazing, but at least with a fast enough computer and for the size of inputs we might reasonably encounter, we have a chance of running them within a human lifetime, and these are regarded as tractable .
However, for algorithms that take , or more steps, the amount of time taken can end up as billions of years even for fairly small problems, and using computers that are thousand times faster still doesn't help to solve much bigger problems.
Such problems are regarded as intractable .
Mathematically, the boundary between tractable and intractable is between a polynomial number of steps (polynomials are formulas made up of , , and so on), and an exponential number of steps (, , , and so on).
The two formulas and look very similar, but they are massively different, and can mean a difference between a few seconds and many millennia for the program to finish.
The whole point of this chapter is to develop an awareness that there are many problems that we have tractable algorithms for, but there are also many that we haven't found any tractable algorithms for.
It's very important to know about these, since it will be futile to try to write programs that are intractable, unless you are only going to be processing very small problems.
Note that algorithms that take a factorial amount of time (, or ) are in the intractable category (in fact, they take times that are a lot worse than ).
Essentially any algorithm that tries out all combinations of the input will inevitably be intractable because the number of combinations is likely to be exponential or factorial.
Thus an important point is that it's usually not going to work to design a system that just tries out all possible solutions to see which is the best.
These algorithms are sometimes called "brute force" - they are simple, and will give the answer, but can take a ridiculous amount of time.
Although we've provided as an example of a tractable time, nearly all algorithms you're likely to encounter will be and better, or and worse – only very specialised ones fall in the gap between those.
So there's a big gulf between tractable and intractable problems, and trying to grapple with it is one of the biggest problems in computer science!
What about Moore's law, which says that computing power is increasing exponentially?
Perhaps that means that if we wait a while, computers will be able to solve problems that are currently intractable?
Unfortunately this argument is wrong; intractable problems are also exponential, and so the rate of improvement due to Moore's law means that it will only allow for slightly larger intractable problems to be solved.
For example, if computing speed is doubling every 18 months (an optimistic view of Moore's law), and we have an intractable problem that takes operations to solve (many take longer than this), then in 18 months we will be able to solve a problem that's just one item bigger.
For example, if you can solve an exponential time problem for 50 items (50 countries on a map to colour, 50 cities for a salesperson to tour, or 50 rings on a Towers of Hanoi problem) in 24 hours, then in 18 months you can expect to buy a computer that could solve it for 51 items at best!
And in 20 years you're likely to be able to get a computer that could solve for 55 items in one day.
You're going to have to be more than patient if you want Moore's law to help out here – you have to be prepared to wait for decades for a small improvement!
Remember that if you need to do calculations of huge numbers, there's a calculator here that you can use: